1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
| import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.art3d import Line3DCollection
np.random.seed(42)
def generate_continuous_fiber(z_base, z_variation, num_fibers, num_segments, step_size, square_size):
lines = []
half_square = square_size / 2 # 正方形边界的一半
for _ in range(num_fibers):
# 在正方形区域内随机选择一个起点
start_point = np.array([
np.random.uniform(-half_square, half_square),
np.random.uniform(-half_square, half_square),
z_base # 初始Z位置设定在z_base加一个小的随机浮动内
])
points = [start_point]
for _ in range(1, num_segments):
while True:
step_direction = np.random.uniform(-1, 1, 3)
step_direction[2] = 0 # 保持Z方向的步长为0,因为我们只希望Z在z_base附近轻微浮动
step = step_size * step_direction / np.linalg.norm(step_direction)
next_point = points[-1] + step
# Z方向上应用非常小的随机浮动
next_point[2] = z_base + np.random.uniform(-z_variation, z_variation)
# 检查新点是否在正方形边界内
if -half_square <= next_point[0] <= half_square and -half_square <= next_point[1] <= half_square:
points.append(next_point)
break # 新点有效,跳出循环
lines.extend([[points[i], points[i+1]] for i in range(len(points) - 1)])
return lines
z_base = 0.5
z_variation = 0.005
num_fibers = 1
num_segments_per_fiber = 8000
step_size = 0.6
square_size = 2.0
lines = generate_continuous_fiber(z_base, z_variation, num_fibers, num_segments_per_fiber, step_size, square_size)
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
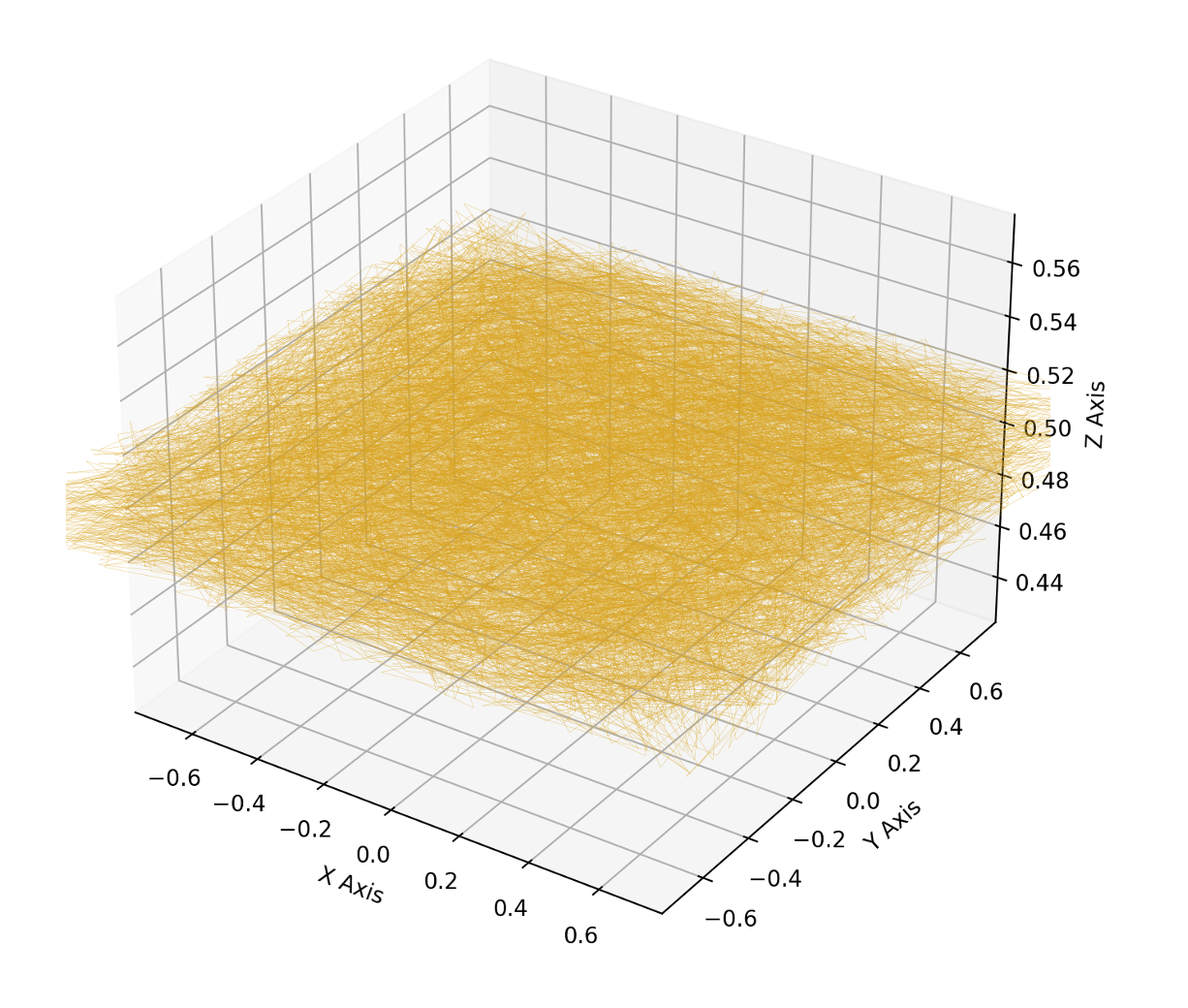
line_collection = Line3DCollection(lines, linewidths=0.1, colors='goldenrod')
ax.add_collection3d(line_collection)
ax.set_xlim([-square_size / 2, square_size / 2])
ax.set_ylim([-square_size / 2, square_size / 2])
ax.set_zlim([z_base - 0.1, z_base + 0.1])
ax.view_init(elev=90, azim=0)
ax.set_xlabel('X Axis')
ax.set_ylabel('Y Axis')
ax.set_zlabel('Z Axis')
plt.show()
|